Вычисление максимального количества точек принадлежащих одной линии из массива точек C#
Дано:
Массив точек на плоскости: points[][] Xi и Yi.
Надо найти:
Сколько максимально точек принадлежит одной прямой.
Пример:
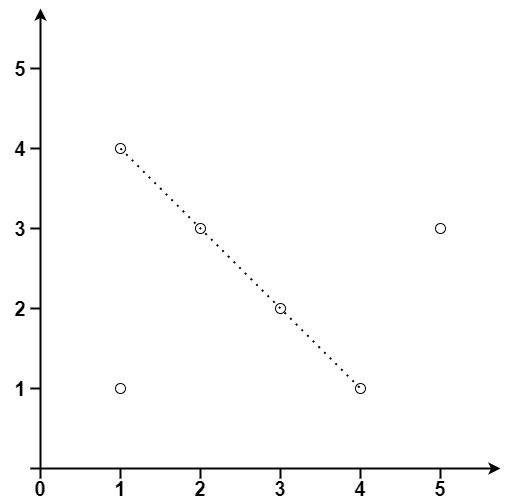
Исходный массив: points= [[1,1],[3,2],[5,3],[4,1],[2,3],[1,4]]
Результат: 4
Пример решения, не лучший, но рабочий:
public int MaxPoints(int[][] points) {
int res = 0;
if (points.Length<3) {return points.Length;}
Dictionary<Tuple<string,int>, string> dict =new Dictionary<Tuple<string, int>, string>();
string formula = "";
decimal k1 = 0;
decimal k2 = 0;
for(int i = 0;i<points.Length-1;i++)
{
for(int k = i+1;k<points.Length;k++){
if(points[i][0]==points[k][0]){
formula = "x="+points[i][0].ToString();
} else if(points[i][1]==points[k][1]){
formula = "y="+points[i][1].ToString();
} else{
k1 = decimal.Round((decimal)(points[k][1]-points[i][1])/(points[k][0]-points[i][0]),10,MidpointRounding.ToZero);
k2 = decimal.Round((decimal)(points[i][0]*points[k][1]-points[i][1]*points[k][0])/(points[k][0]-points[i][0]),10,MidpointRounding.ToZero);
formula = "y="+k1.ToString()+"*x-"+k2.ToString();
}
if(!dict.ContainsKey(new Tuple<string, int>(formula, i))){
dict.Add(new Tuple<string, int>(formula, i),formula);
}
if(!dict.ContainsKey(new Tuple<string, int>(formula, k))){
dict.Add(new Tuple<string, int>(formula, k),formula);
}
}
}
res = dict.GroupBy(x=>x.Value).ToDictionary(grp => grp.Key, grp => grp.Count()).Max(x=> x.Value);
return res;
}Объяснение алгоритма:
Создаем словарь, в котором ключом будет пара [ формула прямой + индекс координат в массиве ].
В значение словаря будем ложить повторно формулу.
Заполняем словарь всеми возможными вариантами формул, для каждой пары точек.
После чего, смотрим какой формулы в словаре больше - это и есть ответ.
Для формулы прямой берем уравнение по двум точкам:
В значение словаря будем ложить повторно формулу.
Заполняем словарь всеми возможными вариантами формул, для каждой пары точек.
После чего, смотрим какой формулы в словаре больше - это и есть ответ.
Для формулы прямой берем уравнение по двум точкам:
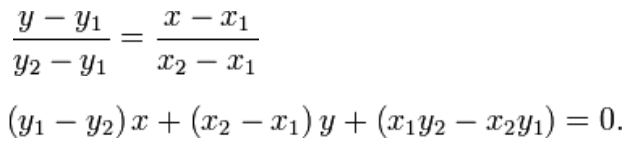
И приводим его к виду с двумя коэффициентами:
Y=kX+b
Где k и b - коэффициенты, в коде выше, вычисляются как переменные k1 и k2.